Nearly every gambler will come across the Martingale System at some point in their lives. The premise is so simple that a large proportion of players will actually ‘invent’ this system themselves. But like most betting systems, the Martingale System is flawed at the most basic level.
What Is the Martingale System?

The Martingale System can be used in many situations, but it is most often associated with roulette. The concept involves betting one outcome of red/black, odd/even or high/low and doubling the amount wagered every time the bet loses.
For example, a player places a bet of $1 on Black. If the outcome of the spin is Black, the player receives $2 – consisting of their $1 bet and a $1 net win. If the outcome of the spin is not Black, the player would lose their $1 stake. On the next spin they would double their bet to $2. Now if the outcome were Black they would win $4 – consisting of their $2 bet, $1 previous bet and $1 net win. If they lose the bet would double to $8, and so on.
As you may be able to see, the net win is limited to the value of the initial bet (in this case $1).
Does It Work?
Martingale System advocates will use the following logic to ‘prove’ the systems validity: The probability of a roulette wheel never coming up black is zero, assuming that the wheel has a fair and unbiased spin. Or to be more accurate, the probability of the result of a roulette wheel never being black approaches zero as the number of spins approaches infinity.
The problem with this logic is that an infinite number of spins requires an infinite amount of money, and a casino willing to take bets of an infinite value. Both of which do not exist.
Lets See The Numbers
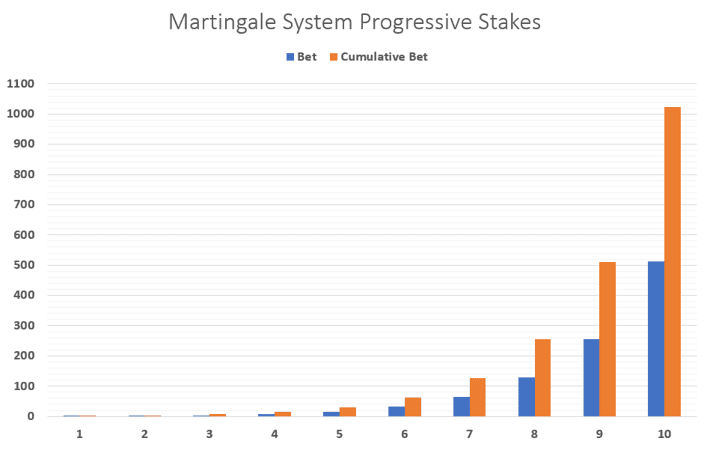
To help you better understand the numbers involved, the table below shows the amount of money required to last for up to 10 spins, doubling each time. Notice that by spin number 10 your initial $1 bet has turned into a bet of $512, and you have racked up total bets of $1,023. Bear in mind that if your $512 bet wins, you still only come out $1 up overall.
| Spin | Bet | Cumulative Bet | Net Win |
|---|---|---|---|
| 1 | $1 | $1 | $1 |
| 2 | $2 | $3 | $1 |
| 3 | $4 | $7 | $1 |
| 4 | $8 | $15 | $1 |
| 5 | $16 | $31 | $1 |
| 6 | $32 | $63 | $1 |
| 7 | $64 | $127 | $1 |
| 8 | $128 | $255 | $1 |
| 9 | $256 | $511 | $1 |
| 10 | $512 | $1,023 | $1 |
In the grand scheme of things, $1,023 isn’t a huge amount of money. And if you had $1,023 to ‘invest’ you may feel (or be conned into thinking) that the Martingale System could work for you. After all, what are the chances of a roulette wheel not coming up black 10 times in a row? Lets find out!
You Cannot Escape The House Edge

As you probably know, there are three colour outcomes on a roulette wheel – red, black and green. As you only win when the outcome is black and lose if it is red or green, your chances of winning are not 50-50. Taking the European ‘single zero’ roulette wheel as an example, your chances of winning are 18 (the number of black segments on a roulette wheel) in 37 (the total number of segments: 18 black, 18 red, 1 green). We can write this as:
P(win) = 18/37
P(win) = 0.486
Which makes the probability of you losing:
P(lose) = 1 – P(win)
P(lose) = 1 – 0.486
P(lose) = 0.514 (can be written as 1 in 1.95)
The probability of you losing two spins in a row can be worked out by taking the probability of one loss and multiplying it against it self, whilst three losses would be the probability of 2 losses multiplies by the probability of one loss, and so on. If we insert this information into the table above it looks like this:
| Spin | Bet | Cumulative Bet | Net Win | Chance of loss |
|---|---|---|---|---|
| 1 | $1 | $1 | $1 | 1 in 1.95 * |
| 2 | $2 | $3 | $1 | 1 in 3.79 * |
| 3 | $4 | $7 | $1 | 1 in 7.38 * |
| 4 | $8 | $15 | $1 | 1 in 14.4 * |
| 5 | $16 | $31 | $1 | 1 in 28.0 * |
| 6 | $32 | $63 | $1 | 1 in 54.5 * |
| 7 | $64 | $127 | $1 | 1 in 106 * |
| 8 | $128 | $255 | $1 | 1 in 207 * |
| 9 | $256 | $511 | $1 | 1 in 403 * |
| 10 | $512 | $1,023 | $1 | 1 in 784 * |
* To 3 significant figures. If you wish to do the calculations yourself, start from the first step and use the un-rounded values.
So as you can see, the chance of you losing 10 spins in a row is approximately 1 in 784. Therefore, for every 784 sets of spins you would expect a run of 10 loses once. Seeing as you make a net win of $1 for every win, and a 10 loss run would cost you $1,023, then in theory for every $783 you win, you would lose $1,023 – making a net loss of $240 (783 winning spin sets minus 1 losing spin set). This assumes that you run out of money after the 10th losing spin and revert back to your initial $1 bet.
But this number comes as no surprise, and is directly related to the house edge. For those of you who are unfamiliar with this term, the house edge is the way in which casino tips the tables in their favour – for roulette this is the zero on the wheel. The house edge of a roulette table with a single zero is 1/37 – approximately 2.7%.
The table below calculates the theoretical total wagers for the 784 roulette spins mentioned above, which comes to $8,868.97. As we know that the house edge for this particular game of roulette is 2.7% we can calculate the expected loss as approximately $240 (to the nearest dollar) – which is the same number that we have already come to.
| Spin | Losses | Wins | Probability (as %) | Number of occurances | Total Stake |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 48.65% | 381.55 | 381.55 |
| 2 | 1 | 1 | 24.98% | 195.93 | 587.79 |
| 3 | 2 | 1 | 12.83% | 100.61 | 704.3 |
| 4 | 3 | 1 | 6.59% | 51.67 | 775 |
| 5 | 4 | 1 | 3.38% | 26.53 | 822.47 |
| 6 | 5 | 1 | 1.74% | 13.62 | 858.33 |
| 7 | 6 | 1 | 0.89% | 7 | 888.52 |
| 8 | 7 | 1 | 0.46% | 3.59 | 916.13 |
| 9 | 8 | 1 | 0.24% | 1.84 | 942.73 |
| 10 | 9 | 1 | 0.12% | 0.95 | 969.16 |
| 10 | 10 | 0 | 0.13% | 1 | 1023 |
| Total: | 8,868.97 |
Bigger Number Mean Bigger Losses
The above examples all assume that you stop after a run of 10 losses. The table below shows the amounts required to be able to withstand a run of 20 losses.
| Spin | Bet | Cumulative Bet | Net Win | Chance of loss |
|---|---|---|---|---|
| 11 | $1,024 | $2,047 | $1 | 1 in 1,527 * |
| 12 | $2,048 | $4,095 | $1 | 1 in 2,974 * |
| 13 | $4,096 | $8,191 | $1 | 1 in 5,792 * |
| 14 | $8,192 | $16,383 | $1 | 1 in 11,280 * |
| 15 | $16,384 | $32,767 | $1 | 1 in 21,965 * |
| 16 | $32,768 | $65,536 | $1 | 1 in 42,773 * |
| 17 | $65,536 | $131,072 | $1 | 1 in 83,295 * |
| 18 | $131,072 | $262,143 | $1 | 1 in 162,206 * |
| 19 | $262,144 | $524,287 | $1 | 1 in 315,874 * |
| 20 | $524,288 | $1,048,576 | $1 | 1 in 615,124* |
* To 0 decimal places.
By 20 losing spins, you have placed cumulative bets of over $1 million! Bear in mind, that all of this is to win $1. A streak of 20 losses should occur approximately once for every 615,124 spins, and for each one of these streaks you lose $1,048,576. Therefore in theory, for every $615,123 you win, you lose $1,048,576 resulting in a net loss of $433,453. Still tempted?
The Casino Has An Insurance Policy: Table Limits
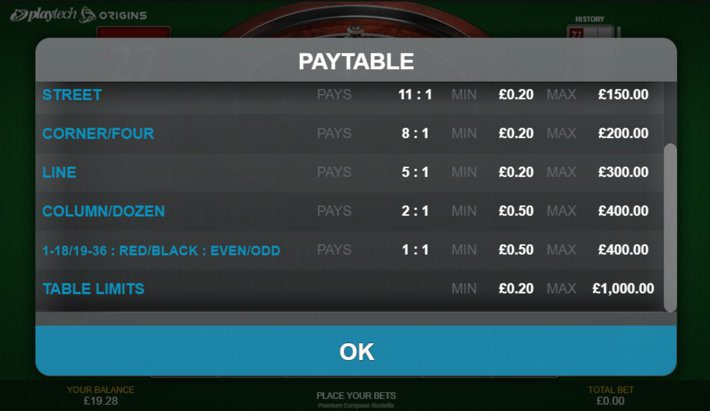
All of the examples above assume a stopping point, such as running out of money – and that is where the Martingale System really falls down. The system only works if you can continue betting if you lose, and in theory if you had enough cash to keep going on forever eventually you would recover your money. But lets say Bill Gates wants to try his hand at the Martingale System and sits down with $50 billion. The casino has an insurance policy against this – table limits.
On most, if not all, roulette tables around the world there will be a table limit – a maximum bet that once reached you cannot increase your bets any further. The maximum bet varies, but it is generally in the region of 500 – 5000 times the minimum bet. This means that, even at the upper end of the lable timit scale, you cannot exceed 13 losing spins.
There really is no system that allows you to “beat” the roulette wheel – if there were, then the game of roulette would cease to exist. You can give yourself a better chance of winning by playing with a bonus – a bonus boosts the amount you have to wager with, allowing you to place more or bigger bets.